VOLTERRY RÓWNANIA CAŁKOWE

równanie całkowe postaci 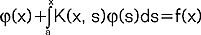, gdzie φ(x) jest szukaną funkcją, K(x, s) - znana funkcja, nazywana jądrem równania całkowego oraz f(x) - znana funkcja (gdy f(x)≠0 - równanie całkowe nazywa się niejednorodne, gdy F(x)≡0 - równanie jednorodne); dla stałej granicy całkowania x=b c.r.V. przechodzi w równanie całkowe Fredholma; c.r.V. jest równaniem całkowym 2-go rodzaju - funkcja niewiadoma j(x) występuje pod znakiem całki oraz poza tą całką (w równaniach 1-go rodzaju φ(x) występuje tylko pod znakiem całki).