POWIERZCHNIOWA CAŁKA

(mat.) dla funkcji f(P) określonej na pewnej powierzchni S c.p. oznacza się symbolem 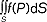i określa wzorem 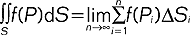, gdzie powierzchnia S została podzielona na elementy powierzchni ΔS_i, a P_i jest dowolnie wybranym punktem wewnątrz ΔS_i; w najprostszym przypadku, gdy powierzchnia zadana jest równaniem jawnym z = z(x, y), c.p. ma postać: 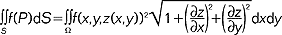, gdzie całkowanie przebiega po Ω - obszarze zmienności zmiennych x, y; w przypadku gdy powierzchnia zadana jest parametrycznie: x = x(u, v), y = y(u, v), z = z(u, v) to: 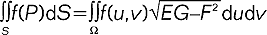, gdzie E(u, v) = x_u² + y_u² + z_u², G(u, v) = x_v² + y_v² + z_v², F(u, v) = x_u x_v + y_u y_v + z_u z_v ( 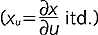itd.), Ω - obszar zmienności parametrów u i v.

• OSTROGRADSKI, Michaił W. (1801-62)...