równanie stopnia trzeciego
równanie algebraiczne postaci x3+ax2+bx+c=0; r. sz. można sprowadzić do postaci zredukowanej (tzw. kanonicznej) z3+pz+q=0 przez podstawienie x=z-a/3; pierwiastki r. sz. zależą od tzw. wyróżnika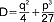 
; 1) gdy D>0, wówczas r.sz. ma pierwiastek rzeczywisty z1 oraz dwa pierwiastki zespolone z2 i z3: 
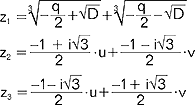gdzie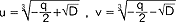 
; 2) gdy D<0 (p wtedy jest ujemne), wówczas r.sz. ma trzy pierwiastki rzeczywiste z1,2,3 dane wzorami: 
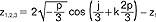dla k=0, z2 dla k=1, z3 dla k=2, gdzie kąt φ wyznacza się ze wzoru: 
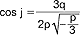; 3) gdy D=0 (p wtedy jest ujemne) wówczas r.sz. ma trzy pierwiastki rzeczywiste, z których dwa są równe: 
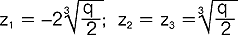; przykład: x3-3x2-4x+12=0 - podstawiając x=z+1 otrzymujemy z3-7z+6=0, wyróżnik 
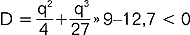równanie ma więc tylko rzeczywiste pierwiastki 
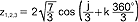, gdzie 
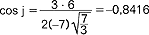oraz φ=147o17', a stąd dla k=0, z1≈2,0 dla k=1 z2≈-3,0, dla k=2 z3≈1,0; dla r.sz. suma pierwiastków z1+z2+z3=0 (2-3+1=0), a ich iloczyn z1z2z3=-q ((2)(-3)(1)=-6); ostatecznie x1=3, x2=-2, x3=2; powyższe równanie można też rozwiązać rozkładając wielomian na czynniki: x3-3x2-4x+12=(x-3)(x+2)(x-2)=0, skąd mamy, jak poprzednio x1=3, x2=-2, x3=2.