UŁAMEK

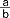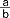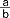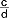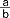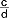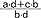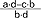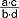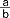(mat.) para liczb zapisana symbolem (lub a/b), gdzie a - licznik, b - mianownik u.; u. można utożsamić z liczbą ułamkową otrzymaną jako wynik dzielenia a przez b (b≠0), czyli jako rozwiązanie równania bx=a; u. jest równy u. wtedy i tylko wtedy, gdy ad = bc; dla dwu u. i można utworzyć ich sumę , różnicę i iloczyn ; u. , w którym a i b są całkowite, przedstawia liczbę wymierną; u. właściwy - u. 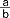w którym a i b są liczbami naturalnymi i a ); u. niewłaściwy - gdy a>b (np. 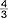); u. nazywamy nieprzywiedlnym (nieskracalnym), gdy jego licznik i mianownik niemają wspólnego czynnika np. 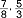, w przeciwnym przypadku u. nazywamy skracalnym (np. 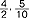); u. piętrowy to ułamek, którego licznik lub mianownik są ułamkami 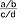(np. 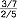); u. piętrowy można przedstawić w postaci 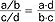; u. dziesiętny to ułamek, którego mianownik jest potęgą liczby 10 i można go przedstawić w postaci liczby dziesiętnej np. 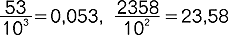; u. dziesiętny nieskończony - rozwinięcie dziesiętne z nieskończoną liczbą cyfr po przecinku np. 3,1415926536..., 0,222...; jeśli w u. dziesiętnym nieskończonym poczynając od pewnego miejsca powtarza się pewna grupa cyfr to u. jest okresowy i przedstawia liczbę wymierną; nieskończone i nieokresowe u. dziesiętne przedstawiają liczby niewymierne, np. 2,7182818285...=e (podstawa logarytmów naturalnych); nazwę u. noszą także wyrażenia postaci f(x)/g(x), gdzie f i g są funkcjami; ludzie posługiwali się u. już w starożytności (Sumerowie, Egipcjanie, Grecy, Indusi, Chińczycy); u. dziesiętne zaczęto używać pod koniec okresu odrodzenia.