ułamki łańcuchowe
(mat.) ułamki postaci: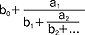 
, gdzie b0, a1, b1, a2, b2,... są dowolnymi liczbami zespolonymi lub rzeczywistymi; gdy u.c. ma nieskończenie wiele ilorazów częściowych 
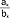nazywa się nieskończonym u.c., w przeciwnym razie u.c. jest skończony; np. dzieląc dwie względnie pierwsze liczby możemy ich iloraz przedstawić za pomocą pewnego skończonego u.c. 
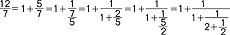; gdy w u.c. nieskończonym odrzucimy ilorazy częściowe począwszy od (k+1)-go otrzymamy skończony u.c. 
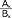nazywany k-tym reduktorem Rk; jeśli ciąg reduktorów jest zbieżny do skończonej granicy, to u.c. nazywa się zbieżny (w przeciwnym razie rozbieżny); jeśli wszystkie ai=1, b0 - całkowite a bi (i≥1) - naturalne, to u.c. nazywa się arytmetyczny; każdą liczbę rzeczywistą można przedstawić w postaci u.c. arytmetycznego, który jest skończony tylko dla liczb wymiernych; pojęcie u.c. wprowadził R. Bombelli (1572) a podstawy teorii u.c. zostały stworzone przez Ch. Huygensa, Lamberta, J.L. Lagrange, L. Eulera (XVII, XVIII w.); idea u.c. dała impuls do wprowadzenia całki Stieltiesa (1894) a obecnie znalazła zastosowanie w obliczeniach komputerowych.
- CIĄGLE, SYNONIM: stale, bezustannie,...