(mat.) liczba przyporządkowana macierzy kwadratowej  stopnia n; w. z macierzy A, oznaczony det A, dany jest wzorem:
stopnia n; w. z macierzy A, oznaczony det A, dany jest wzorem: 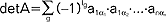 , gdzie
, gdzie  oznacza sumowanie n! składników, a1, ..., an - permutację ciągu 1, 2, ..., n, n! - ilość permutacji tego ciągu, Ig - liczbę inwersji (przestawień) w permutacji g; w każdym składniku sumy we wzorze określającym w. występuje dokładnie jeden element z każdego wiersza i z każdej kolumny macierzy A; np. wyznacznik z macierzy drugiego stopnia -
oznacza sumowanie n! składników, a1, ..., an - permutację ciągu 1, 2, ..., n, n! - ilość permutacji tego ciągu, Ig - liczbę inwersji (przestawień) w permutacji g; w każdym składniku sumy we wzorze określającym w. występuje dokładnie jeden element z każdego wiersza i z każdej kolumny macierzy A; np. wyznacznik z macierzy drugiego stopnia - 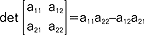 , a w. z macierzy trzeciego stopnia -
, a w. z macierzy trzeciego stopnia - 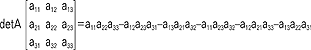 ; w. można inaczej przedstawić w postaci tzw. rozwinięcia Laplace'a: det A = ak1Ak1+ ak2Ak2+ ... aknAkn, gdzie ak1, ... , akn - elementy k-tego wiersza pomnożone są kolejno przez tzw. dopełnienia algebraiczne Ak1, ... , Akn tych elementów (dopełnienie algebraiczne elementu aki to liczba Aki = (-1)k+iMki, Mki jest tzw. podwyznacznikiem otrzymanym z wyznacznika detA przez skreślenie k-tego wiersza i i-tej kolumny przez co obliczanie w. stopnia n sprowadza się do obliczania w. stopni niższych; w. mają następujące ważne własności: 1. jeśli w w. któryś wiersz lub kolumna składają się z samych zer to w. jest równy zeru, 2. zamiana wierszy na kolumny nie zmienia w., 3. zamiana miejscami dwu sąsiednich wierszy lub kolumn powoduje zmianę znaku w., 4. w., w którym dwa wiersze lub kolumny są równe lub proporcjonalne, jest równy zero, 5. gdy cały wiersz lub kolumnę pomnożymy przez liczbę c, to pomnożeniu przez c ulega cały w., 6. det(AB)=det Adet B; w. używa się głównie w teorii równań liniowych.
; w. można inaczej przedstawić w postaci tzw. rozwinięcia Laplace'a: det A = ak1Ak1+ ak2Ak2+ ... aknAkn, gdzie ak1, ... , akn - elementy k-tego wiersza pomnożone są kolejno przez tzw. dopełnienia algebraiczne Ak1, ... , Akn tych elementów (dopełnienie algebraiczne elementu aki to liczba Aki = (-1)k+iMki, Mki jest tzw. podwyznacznikiem otrzymanym z wyznacznika detA przez skreślenie k-tego wiersza i i-tej kolumny przez co obliczanie w. stopnia n sprowadza się do obliczania w. stopni niższych; w. mają następujące ważne własności: 1. jeśli w w. któryś wiersz lub kolumna składają się z samych zer to w. jest równy zeru, 2. zamiana wierszy na kolumny nie zmienia w., 3. zamiana miejscami dwu sąsiednich wierszy lub kolumn powoduje zmianę znaku w., 4. w., w którym dwa wiersze lub kolumny są równe lub proporcjonalne, jest równy zero, 5. gdy cały wiersz lub kolumnę pomnożymy przez liczbę c, to pomnożeniu przez c ulega cały w., 6. det(AB)=det Adet B; w. używa się głównie w teorii równań liniowych.
- cywilizacja, 1. stan i poziom rozwoju...
- wiersz asylabiczny, średniowieczny, najstarszy...
- struktura etniczna ludności świata, jest trudna do ustalenia,...