FOURIERA WZÓR CAŁKOWY

o ile funkcję daną w przedziale (-∞,∞) można pod pewnymi warunkami w każdym skończonym (i tylko skończonym) przedziale (-k, k) przedstawić w postaci szeregu Fouriera, o tyle rozwinięcie jej w szereg Fouriera na całym przedziale określoności funkcji, tj. (-∞,∞), nie jest możliwe. W tej sytuacji stosuje się w.c.F.: 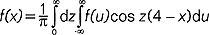Wzór ten otrzymuje się rozwijając najpierw daną funkcję f na skończonym przedziale (-k, k) w szereg Fouriera i przechodząc następnie z k do nieskończoności (k → ∞).