przedstawienie (pod pewnymi ściśle określonymi warunkami) funkcji f danej na skończonym przedziale (-k, k) w postaci sumy nieskończonej następującej postaci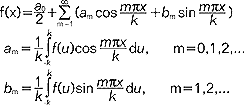 
- nazywa się współczynnikami Fouriera. Takie analityczne przedstawienie funkcji (rozwinięcie jej w szereg Fouriera) ułatwia obliczenia i znajduje duże zastosowanie w fizyce matematycznej (klasyczne przykłady: zagadnienie struny drgającej i zagadnienie rozchodzenia się ciepła w skończonym pręcie), w maszynoznawstwie i elektrotechnice.
DIRICHLETA WARUNKI, FOURIERA WZÓR CAŁKOWY, STEINHAUS, DIRICHLET Peter Gustaw Lejeune, FOURIER Jean Baptiste Joseph, TRYGONOMETRYCZNE SZEREGI
- FOURIERA WZÓR CAŁKOWY, o ile funkcję daną...
- TRYGONOMETRYCZNE SZEREGI, (mat.) szeregi funkcyjne...
- SZEREGI NIESKOŃCZONE, (mat.) wyrażenia dane...