ORTOGONALNA MACIERZ

(mat.) macierz kwadratowa A o wymiarze n, której elementy a_ik spełniają zależność: 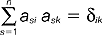, gdzie δ_ik jest funkcją Kroneckera (δ_ik = 0 dla i ≠ k, δ_ik = 1 dla i = k); jeśli utworzymy macierz transponowaną A^T do danej m.o. (tzn. zamienimy wiersze na kolumny i odwrotnie) to spełniony będzie związek AA^T = A^TA = I, gdzie I jest macierzą jednostkową (na przekątnej jedynki, poza przekątną zera); macierz odwrotna do m.o. jest więc równa macierzy transponowanej; przykładem m.o. 2 × 2 jest macierz 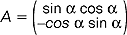; jest to macierz przekształcenia ortogonalnego na płaszczyźnie (zachowującego długość wektorów i kąty między wektorami), którym jest obrót o kąt α.