(mat.) jedna z podstawowych struktur algebraicznych; p. to zbiór P, na którego elementach określone są dwa działania - tzw. dodawanie (+) i mnożenie (), spełniające aksjomaty:
1. a + (b + c) = (a + b) + c - łączność dodawania,
2. a (b c) = (a b) c - łączność mnożenia,
3. a +b = b + a - przemienność dodawania,
4. a (b + c) = a b + a c - rozdzielność mnożenia względem dodawania,
5. dla każdej pary elementów x, y zbioru P istnieje taki element t, że x + t = y (t nazywa się różnicą elementów x - y); p. posiada element neutralny 0 dla dodawania (tzw. zero), taki że dla dowolnego elementu p. x: x + 0 = 0 + x = x; jeśli mnożenie w p. jest przemienne, to p. jest przemienny; jeśli iloczyn dwu elementów niezerowych jest równy zeru (a b = 0 dla a ≠ 0 i b ≠ 0), to a i b nazywamy dzielnikami zera; jeśli istnieje w p. element neutralny mnożenia 1 (nazywamy go jedynką), to dla każdego elementu p.: 1 x = x 1 = x; przykładami p. są: 1) zbiór liczb całkowitych ze zwykłym dodawaniem i mnożeniem; 2) zbiór wielomianów z dodawaniem i mnożeniem; 3) zbiór macierzy 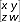 o elementach zespolonych wraz z dodawaniem i mnożeniem tych macierzy; w przykładzie 3) elementem zerowym jest macierz
o elementach zespolonych wraz z dodawaniem i mnożeniem tych macierzy; w przykładzie 3) elementem zerowym jest macierz 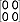 , elementem jednostkowym
, elementem jednostkowym 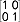 , a dzielnikami zera elementy
, a dzielnikami zera elementy 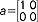 oraz
oraz 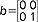 .
.
- pierścień, gonić do pierścienia,...
- pierścień Bishopa, zjawisko meteorologiczne,...
- PIERŚCIEŃ RYBAKA, sygnet używany od...