RÓŻNICZKA

pojęcie matematyczne używane w rachunku różniczkowym; jeśli funkcja y = f(x) ma w punkcie x₀ pochodną f'(x₀), to dla dowolnego h można napisać: f(x+h) - f(x) = f'(x₀)×h +ε(h), przy czym 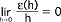obrazek ; r. funkcji f(x) obliczoną w punkcie x₀ dla przyrostu h nazywamy wyrażenie dy = f'(x₀)×h będące liniową funkcją h (przyrost h = dx nazywamy różniczką zmiennej niezależnej x); dla funkcji dwu zmiennych r. definiujemy analogicznie: 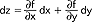obrazek , gdzie 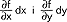obrazek nazywają się r. cząstkowymi (dz jest r. zupełną); r. zupełnej używa się przy szacowaniu błędów, jakimi obarczone są wyniki pomiarów w doświadczeniach fizycznych.