RÓŻNICZKOWY RACHUNEK

dział analizy matematycznej zajmujący się badaniem właściwości, techniką obliczania oraz zastosowaniem pochodnych i różniczek funkcji; podstawowym pojęciem r.r. jest ; dla dwu funkcji f(x) i g(x) posiadających pochodne 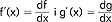obrazek słuszne są następujące wzory, stanowiące podstawowe reguły r.r.: a) [f(x)+g(x)]' = f'(x)+g'(x), b) [f(x) g(x)]' = f'(x) g(x) +f(x) g'(x), c) [c f(x)]' = cf'(x), gdzie c=const, d) 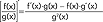obrazek , e) pochodna (względem x) funkcji złożonej y = y(u), gdzie u = u(x): 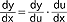obrazek , f) pochodna funkcji odwrotnej: jeśli funkcja x=x(y) ma funkcję odwrotną y=y(x) to pochodna funkcji odwrotnej wyraża się wzorem: 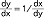obrazek ; powyższe reguły wraz z wzorami na pochodne funkcji elementarnych umożliwiają obliczanie pochodnych wielu złożonych funkcji. Początki r.r. datują się na 2. poł. XVII w., a jego twórcami są I. Newton (który wprowadził pojęcie prędkości jako pochodnej wektora położenia) oraz G.W. Leibniz (dla którego punktem wyjścia było pojęcie stycznej do krzywej); Leibniz wprowadził oznaczenie pochodnej używane do dziś, jest także autorem pojęcia różniczki i pochodnej cząstkowej; pierwsze podręczniki r.r. opublikowali: 1696 G.F.A. de L'Hospital oraz 1748 i 1755 L. Euler; nowe podejście do r.r. (a także rachunku całkowego) było w XIX w. dziełem A.L. Cauchy'ego, B. Bolzana, C.F. Gaussa i K. Weierstrassa.