ZBIEŻNOŚĆ

(mat.) jedno z najważniejszych pojęć w matematyce związane z pojęciem granicy; z. ciągu n elementów a_n (gdzie a_n są liczbami, funkcjami, wektorami itp.) do elementu granicznego g oznacza zmniejszanie się "odległości" między a_n i g dla coraz większych n, co zapisujemy: a_n→g, gdy n→∞; w zależności od sposobu określenia odległości między elementami rozważanego ciągu istnieją różne rodzaje granicy; przykładem może być z. w przestrzeni metrycznej M: w takiej przestrzeni definiuje się funkcję nieujemną ρ(f,g), zwaną metryką przestrzeni M; wtedy ciąg f_nÎM jest zbieżny do elementu fÎM, jeśli 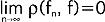, (co zapisuje się f_n→f lub 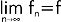; z równości 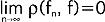wynika równość 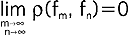ale nie na odwrót (ciąg mający ostatnią właściwość nazywa się ciągiem Cauchy'ego).

wielkość geometryczna charakteryzująca wzajemne położenie przecinających się prostych (np. krawędzi elementu) lub płaszczyzn (np. płaszczyzny gruntu względem płaszczyzny poziomej jako płaszczyzny odniesienia); obliczana jest jako dwukrotność tangensa połowy kąta tworzonego przez te proste lub płaszczyzny; tangens tego kąta zw. jest pochyleniem.

• zbieżność, konwergencja.
• STOCHASTYCZNA ZBIEŻNOŚĆ, zbieżność zachodząca...
• ZBIEŻNOŚĆ KÓŁ POJAZDU, wyrażana w milimetrach...