(mat.) pojęcie pierwotne geometrii; własności p. określają aksjomaty: 1) przez trzy punkty niewspółliniowe przechodzi tylko jedna p.; 2) p. dzieli przestrzeń na dwie części, tzw. półprzestrzenie, o tej własności, że odcinek łączący dwa punkty należące do jednej z tych półprzestrzeni nie przecina p. dzielącej, a odcinek łączący dwa punkty należące do różnych półprzestrzeni przecina p. dzielącą w jednym punkcie; 3) jeśli dwie różne p. mają punkt wspólny, to mają wspólną prostą (krawędź przecięcia tych p.); równanie p. w trójwymiarowej geometrii analitycznej ma postać: ax + by + cz + d = 0 (gdzie a2 + b2 + c2 > 0); współczynniki a, b, c są składowymi wektora prostopadłego do p.; dwie p. o współczynnikach a1, b1, c1, d1 oraz a2, b2, c2, d2 są równoległe, gdy a1/a2 = b1/b2 = c1/c2, prostopadłe zaś, gdy a1a2 + b1b2 + c1c2 = 0; odległość punktu (x0, y0, z0) od p. wyraża się wzorem: 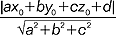 .
.
- płaszczyzna, utworzyć płaszczyznę...
- płaszczyzna ślizgowa, płaszczyzna, względem...
- polaryzacji płaszczyzna, płaszczyzna wyznaczona...