PRAWDOPODOBIEŃSTW ROZKŁADY

(mat.) podstawowe pojęcie rachunku prawdopodobieństwa i statystyki matematycznej odnoszące się do zmiennych losowych, najczęściej liczbowych; r.p. zmiennej losowej X, której dopuszczalne wartości tworzą zbiór skończony lub przeliczalny, określony przez podanie tych wartości x₁, x₂, ... , x_n, ... i odpowiadających im prawdopodobieństw p₁, p₂, ..., p_n, ... (liczby p_i są dodatnie, a ich suma jest równa 1) jest tzw. DYSKRETNYM R.P.; przykładami dyskretnych r.p. są: 1) rozkład dwumianowy (rozkład Bernoulliego) podający prawdopodobieństwo zaobserwowania k sukcesów w n niezależnych doświadczeniach (np. w kolejnych rzutach monetą), z których każde może dać w wyniku sukces lub porażkę; prawdopodobieństwo, że zmienna losowa X = k (k prób zakończy się sukcesem) jest równe: 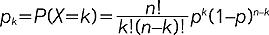obrazek , gdzie p ∈ (0,1), n! = 1 2 3 ... n; 2) rozkład Poissona, określony przez prawdopodobieństwo p_k = P (X = k) = (λ/k!) e^-λ, gdzie k = 0, 1, 2, ..., a parametr λ > 0 oznacza wartość średnią zmiennej losowej; rozkład ten często stosuje się w fizyce i technice do przybliżonego opisu procesów o małym prawdopodobieństwie (np. do obliczania prawdopodobieństwa liczby połączeń w ciągu czasu t w centrali telefonicznej): R.P. CIĄGŁY jest wyznaczony przez przyporządkowanie każdemu przedziałowi (a, b) prawdopodobieństwa, że zmienna losowa X przyjmuje wartość z tego przedziału: P (a ≤ X ≤ b); dla ciągłych zmiennych losowych prawdopodobieństwo to dane jest za pomocą tzw. gęstości prawdopodobieństwa 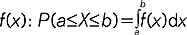obrazek ; przykładami r.p. typu ciągłego są: 1) rozkład normalny (rozkład Gaussa) opisany funkcją gęstości 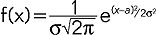obrazek , gdzie a - średnia wartość zmiennej losowej, σ² - wariancja (σ - odchylenie przeciκtne); wielkości losowe o rozkładzie normalnym spotyka się bardzo często, wszędzie tam, gdzie na wynik pomiarów ma wpływ duża liczba niezależnie działających czynników, z których każdy z osobna ma jedynie znikomy wpływ; np. rozkład wartości wszystkich składowych prędkości cząsteczek wykonujących ruchy cieplne; 2) rozkład wykładniczy określony gęstością prawdopodobieństwa f(x) = ae^-ax dla x ≥ 0 i f(x) = 0 dla x < 0, gdzie a < 0 jest stałą; rozkład ten pojawia się przy badaniu emisji cząstek przez substancje radioaktywne; r.p. zmiennych losowych nie ograniczają się do rozkładów dyskretnych i ciągłych, lecz mogą być bardziej skomplikowane; często zamiast całego r.p. (danego np. przy pomocy gęstości lub dystrybuanty) podaje się pewną liczbę parametrów, takich jak wartość przeciętna (wartość średnia) i wariancja (dyspersja); jeżeli dodaje się kilka niezależnych zmiennych losowych to ich suma też będzie zmienną losową o rozkładzie f (x) zależnym od rozkładów składników f₁ i f₂: 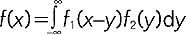obrazek ; rozkład sumy niezależnych zmiennych losowych przy zwiększaniu się liczby składników zbliża się do rozkładu normalnego.