PRAWDOPODOBIEŃSTWO

(mat.) liczba przyporządkowana zdarzeniu, wyrażająca ocenę możliwości zajścia tego zdarzenia w zjawiskach losowych; w matematyce wprowadza się p. w sposób aksjomatyczny (podany przez A.N. Kołmogorowa) następująco: dla każdego doświadczenia (zjawiska losowego) ustalamy zbiór zdarzeń elementarnych Ω (będący pojęciem pierwotnym rachunku prawdopodobieństwa); każde zdarzenie jest wtedy pewnym podzbiorem zbioru Ω, a rodzina S tych podzbiorów spełnia następujące aksjomaty: 1) Ω ∈ S, 2) jeśli zdarzenie A ∈ S to zdarzenie Ω - A ∈ S, 3) jeśli A₁ ∈ S, A₂ ∈ S, ... , to zdarzenie 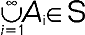. P. nazywa się funkcję rzeczywistą P (A) określoną na zbiorze S (każdemu zdarzeniu A przyporządkowana jest liczba P (A), będąca p. tego zdarzenia) przy czym spełnione są warunki: 1) dla każdego A ∈ S: 0 ≤ P (A) ≤ 1, 2) P (Ω) = 1, (Ω- zdarzenie pewne), 3) p. sumy zdarzeń wykluczających się parami jest równe sumie p. tych zdarzeń 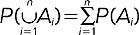; dla wielu zjawisk losowych można wykorzystać tzw. klasyczną definicję p. podaną przez P.S. Laplace'a, według której P(A) = n(A)/N, gdzie n(A) jest liczbą równoprawdopodobnych zdarzeń elementarnych sprzyjających zdarzeniu A, zaś N - liczbą wszystkich zdarzeń elementarnych w danym doświadczeniu; np. przy rzucaniu kostką sześcienną p. wyrzucenia liczby oczek mniejszej od 5 wynosi P(A) = 4/6, bo n(A) = 4 (zdarzeniami sprzyjającymi A jest wyrzucenie jednej z liczb: 1, 2, 3, 4), a N = 6 (wszystkich wyników doświadczenia jest 6).

• prawdopodobieństwo, rachunek prawdopodobieństwa,...
• PRAWDOPODOBIEŃSTWO, SYNONIM: możliwość,...
• PRAWDOPODOBIEŃSTWO LOGICZNE, prawdopodobieństwo metodologiczne...