RIEMANNA FUNKCJA

ζ(z)

analityczna funkcja zmiennej zespolonej z = x + i y (i - jednostka urojona, x, y - liczby rzeczywiste) określona dla x > 1, wprowadzona 1737 przez L. Eulera i dana za pomocą szeregu: 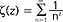; dla f.R. słuszny jest wzór podany przez G.F.B. Riemanna: ζ (1-z) = 2^1-z π^-z Γ(z) ζ (z) cos (πz/2), gdzie Γ(z) jest tzw. funkcją gamma Eulera.

• RIEMANNA CAŁKA, uogólnione przez pojęcie...
• RIEMANNA PRZESTRZEŃ, gładka rozmaitość...
• RIEMANNA-STIELTJESA CAŁKA, uogólnienie całki Riemanna...