gładka rozmaitość M, w której określono tensor metryczny gij dwukrotnie kowariantny, o ciągłych pochodnych - gij jest funkcją określoną na punktach x = (x1, x2,...,xn) rozmaitości M, n jest wymiarem p.R.; tensor gij nazywa się krótko metryką p.R.; istnienie tensora p.R. jest jej podstawową cechą, z której wynika możliwość wprowadzenia w tej przestrzeni pojęć geometrycznych takich, jak długość łuku dowolnej krzywej xi = xi(t), i = 1,...,n, kąt między krzywymi, pole powierzchni obszaru itp.; element długości łuku krzywej określony jest wzorem 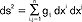 .
.
RIEMANNA GEOMETRIA, ŚLEBODZIŃSKI, GEOMETRIA RÓŻNICZKOWA, CZASOPRZESTRZEŃ
- RIEMANNA GEOMETRIA, uogólnienie klasycznej...
- RÓŻNICZKOWA GEOMETRIA, dział wywodzący się...
- GEOMETRIA RÓŻNICZKOWA, bada obiekty geometryczne...