uogólnienie klasycznej geometrii różniczkowej powierzchni dwuwymiarowych na wypadek wielowymiarowy; idea g.R. polega na wprowadzeniu do rozmaitości n-wymiarowej tensora metrycznego (przestrzeń Riemanna), co umożliwia określenie odległości między sąsiednimi (bliskimi) punktami: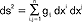 
; g.R. może być zbudowana na formie metrycznej, 
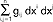, która nie jest określona dodatnio - mamy wtedy do czynienia z pseudoriemannowską przestrzenią, której przykładem jest czterowymiarowa przestrzeń Minkowskiego używana w szczególnej teorii względności (w przestrzeni tej forma pseudometryczna ma postać ds2 = dt2 - (dx2 + dy2 + dz2)/c2, gdzie t - czas, x, y, z - współrzędne przestrzenne, a c - prędkość światła; szczególnymi przypadkami g.R. są: zwykła geometria euklidesowa, geometrie nieeuklidesowe (np. geometria hiperboliczna i eliptyczna); we wszystkich g.R. występują obiekty geometryczne analogiczne, jak w zwykłej geometrii euklidesowej, np. rolę prostych odgrywają geodetyki (krzywe geodezyjne), czyli linie łączące punkty wzdłuż najkrótszej drogi (lub linie o najmniejszej krzywiźnie spośród linii łączących te punkty).
- RÓŻNICZKOWA GEOMETRIA, dział wywodzący się...
- RIEMANN, Georg Friedrich Bernhard...
- GEOMETRIA RÓŻNICZKOWA, bada obiekty geometryczne...