warunek, jaki muszą spełniać szukane (niewiadome) obiekty matematyczne (liczby, funkcje, macierze, figury matematyczne, operatory itp.), zapisany w postaci równości; nazwa r. zależy od natury szukanych obiektów; r. liczbowe, np. x2-4 = 0, r. macierzowe, np.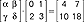 
itd.; rozwiązaniem jest każdy obiekt spełniający warunek zawarty w r. (r. może mieć jedno, kilka lub nieskończenie wiele rozwiązań albo nie mieć rozwiązań wcale); rozwiązanie r. polega na znalezieniu wszystkich jego rozwiązań; r. o jednej niewiadomej x ma postać warunku: f(x) = g(x), gdzie f(x) i g(x) są dwiema funkcjami rozważanymi w części wspólnej ich dziedzin; analogicznie r. o n niewiadomych x1, x2,...,xn ma postać: f(x1, x2,...,xn) = g(x1, x2,...,xn); rozważa się także układy m równań o n niewiadomych; gdy funkcje f(x) i g(x) są wielomianami, to r. f(x) = g(x) nazywa się algebraicznym, a jeśli f(x) lub g(x) jest przestępna, to r. nazywa się przestępnym; w geometrii przez r. rozumiemy warunek, jaki mają spełniać elementy szukanego obiektu geometrycznego, zapisany w formie odpowiedniej równości, np. (x+1)2+(y-2)2 = 9 jest r. okręgu o środku (-1, 2) i promieniu 3; x -2y + z = 1 jest r. płaszczyzny w przestrzeni trójwymiarowej itp.; dwa r. posiadające jednakowe zbiory rozwiązań nazywamy r. równoważnymi, np. x2-4 = 0 i (x-2)(x+2) = 0 są r. równoważnymi.
- równanie, lewa strona równania,...
- równanie Clapeyrona, Clapeyrona równanie.(...)
- SZEŚCIENNE RÓWNANIE, równanie stopnia trzeciego...