SZEREGI NIESKOŃCZONE

(mat.) wyrażenia dane w postaci sumy nieskończonej liczby składników: a₁+a₂+...+a_n+... lub krótko 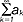obrazek ; rozróżniamy sz.n. liczbowe (wszystkie składniki szeregu są liczbami) i funkcyjne (wszystkie składniki są funkcjami); sumę n pierwszych składników nazywamy n-tą sumą częściową sz.n.: S_n=a₁+a₂+...+a_n; liczbowy sz.n. jest zbieżny, jeśli ciąg sum częściowych {S_n} jest zbieżny do granicy 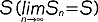obrazek i wtedy piszemy krótko: 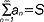obrazek ; sz.n., który nie jest zbieżny, nazywa się rozbieżnym; przykładem liczbowego sz.n. zbieżnego do liczby π/4 jest szereg: 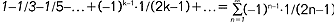obrazek , a rozwinięcie funkcji 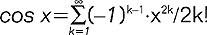obrazek jest przykładem funkcyjnego sz.n. zbieżnego; przykładem rozbieżnego liczbowego sz.n. jest szereg: 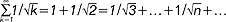obrazek ; sz.n. 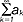obrazek jest bezwzględnie zbieżny, gdy sz.n. zbudowany z wartości bezwzględnych jest zbieżny 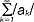obrazek ; w celu zbadania, czy dany szereg jest zbieżny czy nie, używamy tzw. kryteriów zbieżności; sz.n. funkcyjny jest zbieżny do funkcji f(x), gdy ciąg sum częściowych S_n(x)=f₁(x)+...+f_n(x) jest zbieżny do funkcji f(x); w szczególności, gdy zbieżność ciągu {S_n} jest jednostajna, to sz.n. funkcyjny nazywamy jednostajnie zbieżnym do f(x); w wielu działach matematyki, a także zastosowaniach technicznych dużą rolę odgrywają następujące funkcyjne sz.n.: szereg Taylora, szereg Maclaurina, szeregi trygonometryczne, szeregi Fouriera; sz.n. zostały wprowadzone do matematyki przez I. Newtona; pierwszy podręcznik nt. sz.n. napisał w XVII w. J. Bernoulli; badanie sz.n. w dziedzinie liczb zespolonych zapoczątkował L. Euler.