TRYGONOMETRYCZNE FUNKCJE

(mat.) funkcje kąta φ (sinus, cosinus, tangens, cotangens, secans i cosecans) określone następująco: sinφ=y/r, cosφ=x/r, tgφ=y/x=sinφ/cosφ (dla φ≠90°n180°, n=1, 2, 3), ctgφ=x/y=cosφ/sinφ (dla φ≠n180°); secφ=r/x=1/cosφ (dla φ≠90°n180°), cosecφ=r/y=1/sinφ (dla φ≠n180°), gdzie x, y są współrzędnymi punktu P, r - promień koła, a kąt φ - kąt między dodatnim ramieniem osi OX a odcinkiem OP; kąt φ można wyrażać w stopniach lub radianach - kąt α° ma miarę απ/180 radianσw; wykresy f.t. są pokazane na rysunku; f.t. są funkcjami okresowymi - funkcje sin, cos, sec, cosec mają okres 360° (2π rad) a tg i ctg - 180° (π rad); f.t. dowolnego kąta można znaleźć na podstawie znajomości tych funkcji dla kątów φ należących do pierwszej ćwiartki tzn. 0≤φ≤90° oraz tzw. wzorów redukcyjnych: sin(φ+kπ)=sinφ, cos(φ+kπ)=cosφ, tg(φ+kπ)=tgφ, ctg(φ+kπ)=ctgφ, gdzie k - liczba całkowita, przy czym górny znak odpowiada k=2n, a dolny k=2n+1, n - liczba naturalna, sin(φ+kπ/2)=cosφ, cos(φ+kπ/2)=sinφ, tg(φ+kπ/2)=ctgφ, gdzie k - liczba całkowita nieparzysta oraz górny znak odpowiada k=4n+1 a dolny - k=4n-1; podstawowy związek dla f.t. ma postać: cos²φ+sin²φ=1 dla dowolnego kąta φ; inne zaleności dla f.t. to: 1). wzory wyrażające f.t. sumy lub różnicy kątów poprzez f.t. tych kątów: sin(αβ)=sinαcosβcosαsinβ, cos(αβ)= cosαcosβsinαsinβ 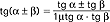obrazek , gdzie znaki gσrne (i dolne) lewej części każdego wzoru odpowiadają znakom górnym (i dolnym) prawej części wzoru; 2).wzory na sumę (lub różnicę) f.t. (Regiomontanus, XV w., J. Napier XVII w.): 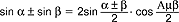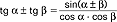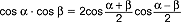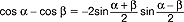obrazek , obrazek , obrazek , obrazek ; 3).f.t. można przedstawić w postaci szeregów potęgowych zbieżnych dla każdego kąta α, np. 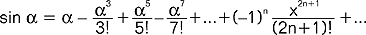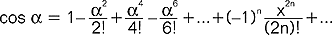obrazek , obrazek (analogiczne wzory istnieją dla pozostałych f. t.); funkcje odwrotne do f.t. nazywają się funkcjami kołowymi (lub cyklometrycznymi); pierwsze pojęcia dotyczące f.t. powstały w starożytnej Grecji (Euklides, Archimedes, Apoloniusz z Pergi i in.); pierwsza tablica sinusów powstała w II w. (Ptolemeusz Klaudiusz); Arjabhata znał tożsamość cos²α+sin²α =1; obecnie istniejąca postać teorii f.t. stworzona została przez L. Eulera (XVIII w.), który m.in. wprowadził definicje f.t. dla argumentów zespolonych z, odkrył związek f.t. z funkcją wykładniczą e^z (tzw. wzory Eulera) oraz wykazał ortogonalność układu funkcji 1, cosα, sinα, cos2α, sin2α,...; f.t. są stosowane w wielu gałęziach fizyki szczególnie przy opisie zjawisk okresowych (np. wszelkiego rodzaju drgań).