TRYGONOMETRYCZNE SZEREGI

(mat.) szeregi funkcyjne o postaci: 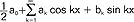obrazek gdzie a₀, a_k, b_k - stałe liczby rzeczywiste będące współczynnikami sz.t.; jeśli funkcje cos kx i sin kx zastąpimy zgodnie z wzorem Eulera e^ikx=coskxisinkx funkcjami e^ikx oraz , e^-ikx to sz.t. przyjmie postać: 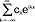obrazek , gdzie i=√-1, 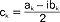obrazek dla k≥0 oraz 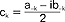obrazek dla k<0; sz.t. określony wyżej ma okres 2π - sz.t. o innym niż 2π okresie można sprowadzić do powyższej postaci; jeżeli szereg powyższy jest zbieżny w przedziale [0, 2π], to jest zbieżny dla wszystkich x i jego suma jest funkcją okresową f(x)=f(x+2π); sz.t. odgrywają ważną rolę, bo można przy ich pomocy przedstawić w przedziale [0, 2π] funkcje w pewnej mierze dowolne (prócz tego przedział [0, 2π] można zastąpić dowolnym przedziałem [a, b] podstawiając w sz.t. 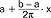obrazek za zmienną x); w szczególności gdy f(x) jest funkcją całkowalną w przedziale [0, 2π] to można dla niej zbudować tzw. szereg Fouriera postaci: 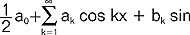obrazek , gdzie 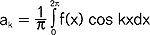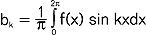obrazek , obrazek ; nawet gdy szereg Fouriera funkcji f(x) jest zbieżny, nie zawsze jest równy funkcji f(x) (funkcje, które są równe swoim szeregom Fouriera, odgrywają szczególnie ważną rolę w zastosowaniach w fizyce matematycznej); rozwój teorii sz.t. był powiązany z określeniem takich pojęć jak funkcje, całki oraz powstawaniem i rozwijaniem się takich dziedzin matematyki jak teoria mnogości , teoria funkcji rzeczywistych, analiza funkcjonalna; sz.t. były używane już przez L. Eulera (ok. 1748); J. Fourier (ok. 1811) stosował sz.t. do opisu przewodnictwa cieplnego; sz.t. zajmowali się także B. Riemann, G. Cantor i H. Lebesgue.