TRYGONOMETRIA

dział matematyki zajmujący się własnościami funkcji trygonometrycznych i ich zastosowaniami w geometrii płaskiej i sferycznej (w szczególności do rozwiązywania trójkątów); t. płaska (euklidesowa) bada związki w trójkątach (także wielokątach) na płaszczyźnie; dla trójkąta o bokach a, b, c i kątach α, β, γ leżących naprzeciw tych boków podstawowe wzory t. płaskiej to: wzór sinusów - 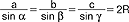obrazek (Nasir ad-Din, XIII w), wzór cosinusów a²=b²+c²-2bccosα, b²=a²+c²-2accosβ, c²=a²+b²-2abcosγ (po raz pierwszy w Elementach Euklidesa), wzory tangensσw 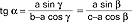obrazek (oraz analogiczne wzory dla tgβ i tgγ), wzory na pola trójkąta S=(1/2)absinγ=(1/2)bcsinα=(1/2)acsinβ, wzory wiążące kąty trójkąta z jego bokami 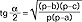obrazek (oraz analogiczne wzory dla pozostałych kątów); t. sferyczna zajmuje się związkami w trójkątach na powierzchni kuli; dla trójkąta sferycznego o kątach płaskich α, β, γ oraz bokach, ktσrych miarą są odpowiednie kąty środkowe a, b, c (wtedy długości boków trójkąta są: aR, bR, cR, gdzie R - promień kuli) prawdziwe są wzory: wzór sinusów 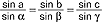obrazek (Abu'l-Wefa, X w.), wzór cosinusów dla boków: cosa=cosbcosc+sinbsincsinα (Regiomontanus, XV w.), wzór cosinusów dla kątów: cosα=-cosβcosγ+sinβsinγcosα (F. Vite, 2 poł. XVI w.) (wzory dla pozostałych boków i kątów otrzymujemy przestawiając cyklicznie α→β→γ→α oraz a→b→c→a); t. płaską zajmowali się al-Battani (IX-X w.), Abu'l-Wefa, A. Bhaskara, Nasir ad-Din, później M. Kopernik, Tycho de Brahe, J. Kepler; t. sferyczna powstała wcześniej niż płaska (znajdując zastosowanie w astronomii); zajmowali się nią Menelaos z Aleksandrii, Ptolemeusz Klaudiusz; pełny zestaw wzorów t. sferycznej podał L. Euler, który też nadał ostateczny kształt t. płaskiej; t. istnieje także w geometriach nieeuklidesowych - w geom. hiperbolicznej (Łobaczewskiego) i eliptycznej (Riemanna).