WARIACYJNY RACHUNEK

(mat.) dział analizy mat. zajmujący się badaniem ekstremów funkcjonałów; typowy problem r.w. polega na znalezieniu takiej różniczkowalnej funkcji x(t) (zadanej dla t=t₁ i t=t₂), dla której funkcjonał 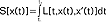obrazek (gdzie X'(t)=dx/dt) przyjmuje wartość najmniejszą lub największą, przy czym L jest daną funkcją argumentów t, x, x' a x(t) - szukaną funkcją; można udowodnić, że jeśli funkcjonał S przybiera ekstremum dla funkcji x(t), to funkcja ta spełnia równanie różniczkowe; 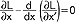obrazek Eulera-Lagrange'a (spełnienie tego równania przez szukaną funkcję x(t) jest więc warunkiem koniecznym istnienia ekstremum funkcjonału S); równania fizyki matematycznej mają zwykle postać równań Eulera-Lagrange'a a procesy opisane przez te równania przebiegają tak, by odpowiadający im funkcjonał przybierał ekstremum; r.w. znalazł też zastosowanie w technice, zwłaszcza w teorii optymalnego sterowania układami, gdzie poszukuje się ekstremum pewnego funkcjonału J[x(t),y(t)] zależnego od dwu funkcji: x(t) opisującej układ i y(t) opisującej proces sterowania, przy czym często udaje się znaleźć jedynie przybliżone rozwiązanie; pierwszym rozwiązanym zagadnieniem r.w. było tzw. zagadnienie brachistochrony (Johann i Jacob Bernoulli, 1696), przy czym odpowiedni funkcjonał ma postać: 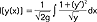obrazek ; zagadnieniami r.w. zajmowali się też M.W. Ostrogradski, C.F. Gauss, A.M. Legendre, K. Weierstrass i inni.