WEKTOROWY RACHUNEK

(mat.) dział matematyki zajmujący się właściwościami wektorów i ich zastosowaniami w geometrii, fizyce i technice; 1. w algebrze wektorowej zbiór wektorów ma właściwości przestrzeni wektorowej (wektory można dodawać, odejmować, mnożyć przez liczby - wynikiem każdej z tych operacji jest nowy wektor: 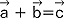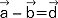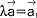obrazek , obrazek , obrazek ); kombinacją liniową wektorów 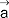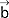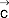obrazek , obrazek , obrazek nazywamy wyrażenie postaci: 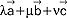obrazek (λ, μ, ν - liczby); wektory 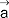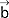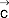obrazek , obrazek , obrazek , nazywamy liniowo niezależnymi, jeśli z warunku 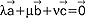obrazek wynika, że λ=μ=ν=0; jeśli zaś istnieją takie trzy liczby λ, μ, ν, że λ²+ μ²+ ν²≠0 oraz 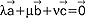obrazek , wtedy wektory 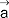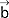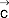obrazek , obrazek , obrazek są liniowo zależne, tzn. każdy z nich da się przedstawić jako pewna liniowa kombinacja pozostałych; w przestrzeni trójwymiarowej trzy wektory leżące na jednej płaszczyźnie oraz każde cztery wektory są liniowo zależne; trzy wektory 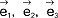obrazek liniowo niezależne i o wspólnym początku w przestrzeni trójwymiarowej tworzą tzw. bazę tej przestrzeni, tzn. dowolny wektor 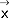obrazek da się przedstawić jako ich kombinacja liniowa: 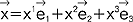obrazek (liczby - x¹, x², x³ współrzędne wektora w bazie e₁, e₂, e₃); przykładem bazy jest trójka wersorów osi OX, OY, OZ - 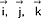obrazek ; 2. w analizie wektorowej bada się pola skalarne i wektorowe oraz pewne operacje różniczkowe i całkowe określone na tych polach; najważniejsze operacje różniczkowe to gradient, dywergencja i rotacja: 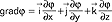obrazek (φ - pole skalarne), 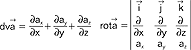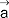obrazek , ( obrazek - pole wektorowe); najważniejsze operacje całkowe używane w r.w. to: krążenie pola wektorowego ( 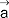obrazek (P) wzdłuż zamkniętego konturu L - 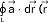obrazek - wektor wodzący punktu na konturze L), strumień pola wektorowego ( 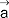obrazek (P) przez powierzchnię S - 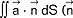obrazek - wektor normalny do powierzchni S); związki między poszczególnymi operacjami całkowymi i różniczkowymi określone są przez podstawowe twierdzenia r.w. - tw. Greena, tw. Gaussa-Ostrogradskiego, tw. Stokesa, szeroko stosowane w fizyce i technice; r.w. zajmowali się w XIX w. H.G. Grassmann, W.R. Hamilton, J.C. Maxwell, J.W. Gibbs, przyczyniając się do stworzenia z niego odrębnej gałęzi matematyki.