(mat.) uogólnienie pojęcia wektora i skalara; t. jest wielkością zmieniającą się przy zmianie układu współrzędnych w specjalny sposób: jeśli w pewnym układzie współrzędnych U punkt P ma współrzędne x1,x2,...,xn, to współrzędne tego punktu w innym układzie U' - x'1,x'2,...,x'n można traktować jako funkcje starych współrzędnych tzn. x'r=x'r(x1,x2,...,xn), gdzie r=1, 2, ...,n; funkcje x'r są ciągłe, różniczkowalne i wzajemnie jednoznaczne; skalarem (tensorem zerowego rzędu) jest taka funkcja punktu P, że φ(x1,x2,...,xn)=φ'(x'1,x'2,...,x'n) (dokładniej: φ jest polem skalarnym); wektorem kontrawariantnym vi (wskaźnik i u góry) nazywamy taką wielkość, której współrzędne v1,v2,...,vn przy przekształceniach układu współrzędnych transformują się zgodnie z prawem: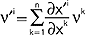 
; analogicznie jeśli 
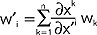to zespół wielkości w1,w2,...,wn stanowi wektor kowariantny (wskaźniki i u dołu); wektory kontra- i kowariantne są t. rzędu pierwszego; zbiór wielkości Trs jest zbiorem składowych tensora kontrawariantnego drugiego rzędu, jeśli wielkości te transformują się zgodnie z równaniami: 
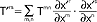; analogicznie dla tensora kowariantnego drugiego rzędu prawo transformacji ma postać: 
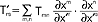; przykładem tensora mieszanego jest zbiór wielkości T'str transformujących się według prawa: 
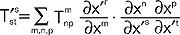; powyższe definicje łatwo uogólniają się na tensory wyższych rzędów α-krotnie kontra- i β-krotnie kowariantne; prototypem wektora kowariantnego jest pochodna cząstkowa niezmiennika, a prototypem wektora kontrawariantnego jest przemieszczenie infinitezymalne (nieskończenie małe); iloczyn urvs dwóch wektorów kontrawariantnych ur i vs jest tensorem kontrawariantnym drugiego rzędu; dwa tensory tego samego rzędu i rodzaju dodane do siebie tworzą inny tensor; właściwościami t. zajmuje się rachunek tensorowy.
- RIEMANNA PRZESTRZEŃ, gładka rozmaitość...
- RIEMANNA GEOMETRIA, uogólnienie klasycznej...
- naprężenie mechaniczne, miara sił wewnętrznych...