CAŁKA OZNACZONA

pojęcie z zakresu analizy matematycznej, którego idea wyrosła z potrzeby obliczania pól dowolnych figur (a także objętości brył, długości krzywych i innych wielkości). Podstawowym pojęciem jest c.o. funkcji jednej zmiennej f(x), tzn. c.o. pojedyncza. Jeśli f(x) jest określona i ograniczona w przedziale [a, b] to jej c.o. w tym przedziale otrzymujemy następująco: przedział [a, b] dzielimy punktami x₁, x₂,..., x_i, x_i+1,..., x_n-1 na przedziały Δx₁, Δx_2,,... Δx_n tak aby przy zwiększającej się liczbie punktów podziału n długość największego z odcinków Δ x_i - δ_n była coraz mniejsza (mówimy, że ciąg podziałów jest ciągiem normalnym, gdy granica δ_n przy nξA jest równa zero). Następnie w każdym z przedziałów Δ x_i wybieramy punkt pośredni ξ_i i tworzymy sumę A = f(ξ₁) Δ x₁ + f(ξ₂) Δ x₂ +... + f(ξ_n) Δ x_n. Dla funkcji przedstawionej na rysunku widać, że f(_i) Δ x_i jest polem prostokąta o bokach Δ x_i i f(ξ_i), a suma A - łącznym polem prostokątów o podstawach Δ x₁, Δ x₂,..., Δ x_n i wysokościach f(ξ₁), f(ξ₂),..., f(ξ_n). Dla tzw. funkcji całkowalnej każdemu sposobowi podziału odcinka [a, b] oraz każdemu wyborowi punktów pośrednich ξ_i odpowiada inna suma A_k, ale ciąg tych sum {A_k} jest zbieżny do tej samej wartości zwanej c.o. funkcji f(x) w przedziale [a, b], oznaczonej symbolem 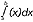, gdzie liczby a i b nazywamy granicami całkowania a f(x) - funkcją podcałkową. C.o. znajdują bardzo szerokie zastosowanie w naukach podstawowych i stosowanych oraz technice. W obliczeniach c.o. wykorzystuje się często ich własność zw. addytywnością całki, która pozwala zastąpić całkowanie po określonym obszarze znacznie łatwiejszym całkowaniem po częściach tego obszaru.

RIEMANNA CAŁKA, CAŁKA, SIMPSON

• CAŁKA NIEOZNACZONA, całka nieokreślona
• NIEOZNACZONA CAŁKA, (mat.) .
• STIELTJESA CAŁKA, uogólnienie pojęcia...