krzywa płaska (jedna ze stożkowych) stanowiąca zbiór punktów (M) płaszczyzny, których suma odległości od dwóch stałych i różnych punktów (F1, F2) tej płaszczyzny jest stała i większa od odległości między tymi punktami. Punkty te zwane są ogniskami, odległość między nimi (2c) nazywamy odległością ogniskową e., środek zaś (O) odcinka o końcach w ogniskach e. - środkiem e. Jest to jedyny środek symetrii e., natomiast wśród osi symetrii e. wyróżnić należy jedną (l1), przechodzącą przez ogniska e. i drugą (l2), do niej prostopadłą i przechodzącą przez środek e. Odcinek (AB, o długości 2a) łączący punkty przecięcia pierwszej z tych osi symetrii z e. nazywa się osią wielką e., odcinek (CD, długości 2b) zaś łączący punkty przecięcia drugiej osi symetrii z e. - osią małą e. Punkty przecięcia obu osi symetrii e. z e. noszą nazwę wierzchołków elipsy. Długości (r1, r2) odcinków F1M i F2M nazywa się promieniami wodzącymi punktu M e.; ich suma równa jest długości osi wielkiej e.: r1 + r2 = 2a. Wartość ilorazu ogniskowej i osi wielkiej e., 2c/2a, nazywa się mimośrodem e.; jest to liczba nieujemna mniejsza od 1 (dla okręgu równa 0). Kierownicą e. nazywamy prostą, taką że stosunek odległości dowolnego punktu e. od ogniska do odległości tego punktu od tej prostej jest stały i równy mimośrodowi e. E. ma dwie kierownice (k1, k2), każda odpowiada jednemu ognisku e. Średnicami e. nazywa się jej cięciwy (odcinki o końcach leżących na e.) przechodzące przez środek e. Normalna (n) do e. w punkcie M. jest dwusieczną kąta między promieniami wodzącymi tego punktu. Promienie świetlne wychodzące z jednego ogniska e., po idealnym odbiciu od elipsy, skupiają się w drugim jej ognisku. W kartezjańskim układzie współrzędnych, w którym e. jest zbiorem punktów o współrzędnych (x,y) oraz gdy osie układu pokrywają się z osiami e. (oś x z osią wielką), równanie e. ma postać: x2/a2 + y2/b2 = 1, (a>0, b>0), przy czym c2 = a2 - b2, c>0, kierownice zaś mają równania: x = -a2/c, x = a2/c. W tym samym układzie współrzędnych e. można opisać tzw. równaniami parametrycznymi: x = a cos u, y = b sin u, gdzie u Î á0; 2πń - kąt, zwany anomalią punktu, zawarty pomiędzy odcinkiem o końcach w środku O i punkcie M. elipsy o współrzędnych (x,y) a osią x. Pole e. określa wzór Pe = πab, a jej
obwód wzór przybliżony 
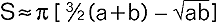. Do kreślenia e. służą elipsografy.
KRZYWA, KEPLERA PRAWA, JODRELL BANK OBSERVATORY, WYRZUTNIA, WSPÓŁOGNISKOWY, STOŻKOWE, ORBITA, LISSAJOUS FIGURY, STOŻKA PRZEKROJE, APOLONIUSZ
- ELIPSA, wyrzutnia
- elipsa, (gr. lleipsis = brak,...
- zdanie eliptyczne, (gr. elipsa = powtórzenie...