OSTROGRADSKIEGO-EULERA RÓWNANIE

(mat.) równanie używane w rachunku wariacyjnym badane przez M.W. Ostrogradskiego (1850) (jest ono równaniem typu Lagrange'a-Eulera); np. rozważanie problemu znalezienia minimalnej powierzchni rozpiętej na danej krzywej zamkniętej w przestrzeni prowadzi do r.O.-E. (tzw. problem powierzchni minimalnych); w najprostszym przypadku dwu zmiennych x, y r.O.-E. jest równaniem różniczkowym postaci ∂F/∂z-∂/∂x(∂F/∂z_x)-∂F/∂z-∂/∂y(∂F/∂z_y)=0, gdzie z(x, y) jest szukaną funkcją nadającą wartość ekstremalną funkcjonałowi I(z (x, y))= 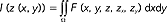F (x, y, z, z_x, z_y) dxdy, (z_x=∂z/∂x, z_y=∂z/∂y).