pozwala (pod pewnymi warunkami dotyczącymi regularności funkcji i własności obszaru) na zamianę całki objętościowej (potrójnej) na całkę powierzchniową (podwójną); wygodny i często stosowany w matematyce i fizyce wzór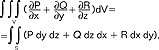 
, gdzie S jest powierzchnią zorientowaną ograniczającą obszar trójwymiarowy V, natomiast Q, P, R są ciągłymi funkcjami trzech zmiennych określonymi w obszarze jednospójnym, zawierającymi powierzchnię S.
OSTROGRADSKIEGO-GAUSSA WZÓR, WEKTOROWY RACHUNEK, OSTROGRADSKI